A collaborative effort.
A collaborative effort.
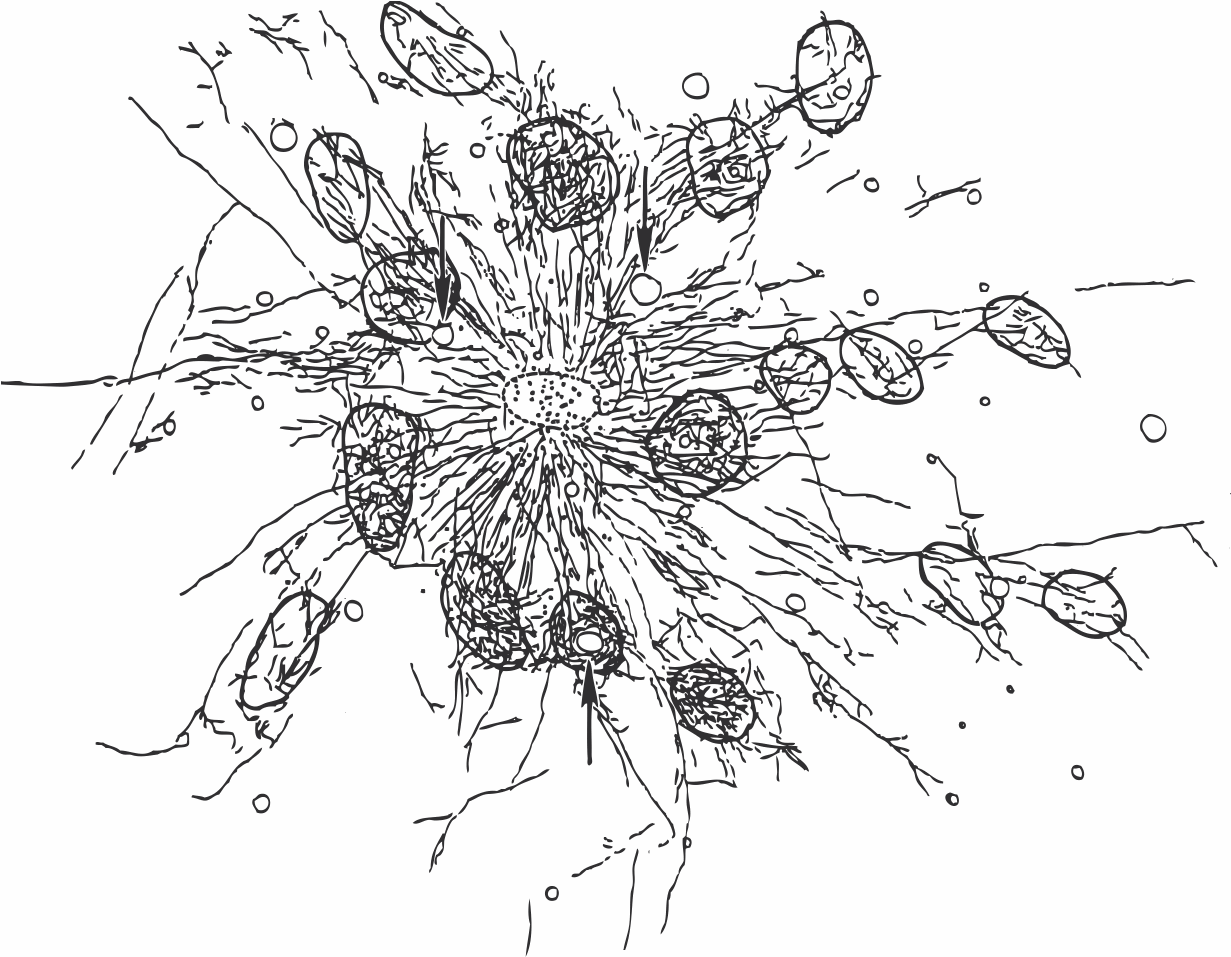
When injections of dye are made into the upper layers of cortex, a remarkable structure of neuronal connectivity is revealed. Dye is absorbed by neurons and transported along axons and dendrites to fill entire cells. When a large population of neurons is stained in this way, slices examined in tangential section show a semi-regular array of denser staining.
By default, Matlab matrices must be fully loaded into memory. This can make allocating and working with huge matrices a pain, especially if you only really need access to a small portion of the matrix at a time. memmapfile allows the data for a matrix to be stored on disk, but you can't access the matrix transparently in functions that don't expect a memmapfile object without reading in the whole matrix. MappedTensor is a matlab class that looks like a simple matlab tensor, with all the data stored on disk.
View from the hotel
View from the hotel
We spent a fascinating two weeks at Capo Caccia discussing winner-take-all competition in relation to cortical anatomy, and began a collaboration examining transient sycnhrony in cortical networks.
The Alpha hull of a set of random points
The Alpha hull of a set of random points