Lateral competition in cortex
Can local inhibition lead to long-range competition?
20th February, 2014Figure 1: Presence of competition in a local-inhibition network

Figure 1: Presence of competition in a local-inhibition network
Figure 2: Mexican hats and cortical anatomy
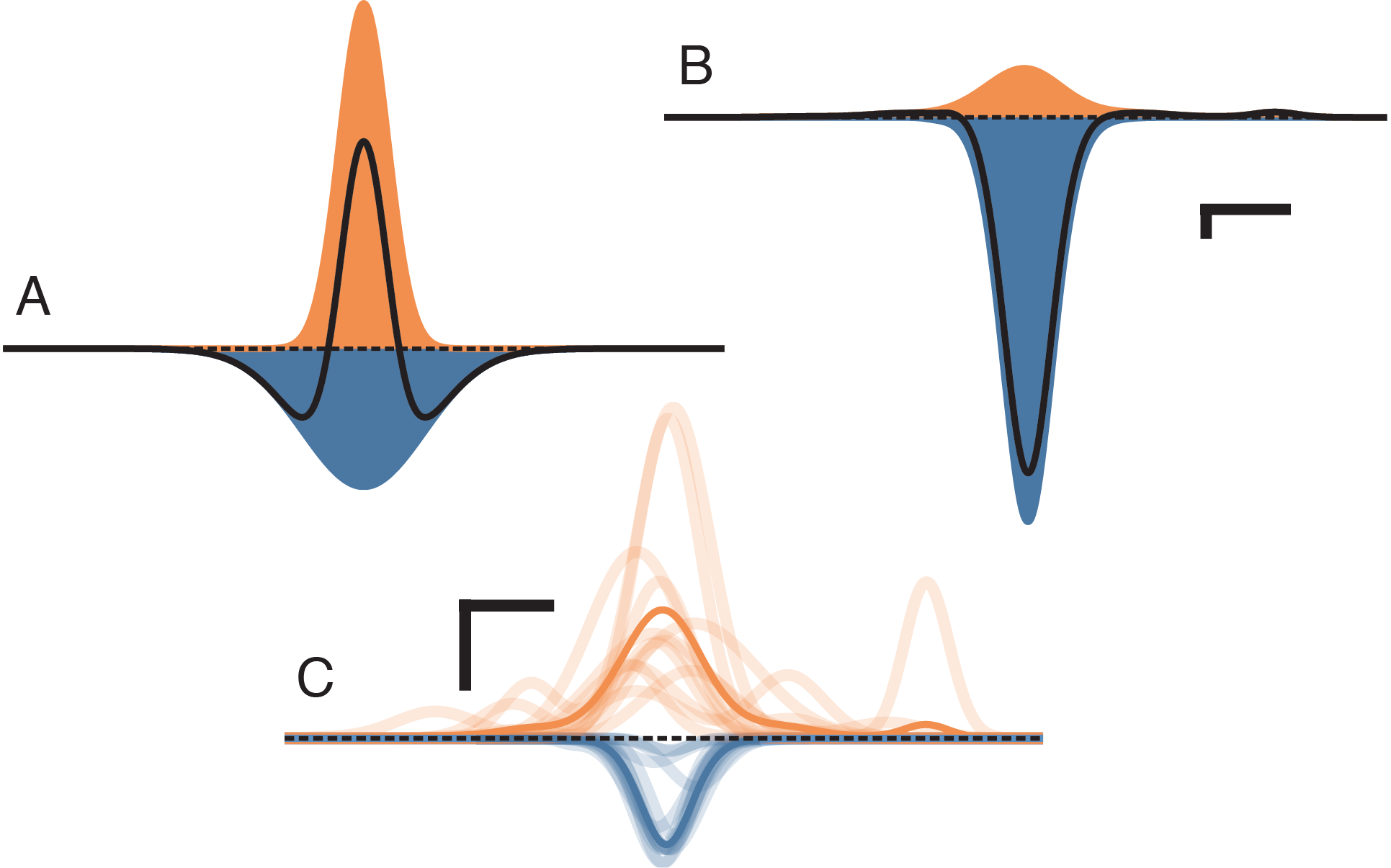
Figure 2: Mexican hats and cortical anatomy
Figure 3: Analytical models for competition in cortex
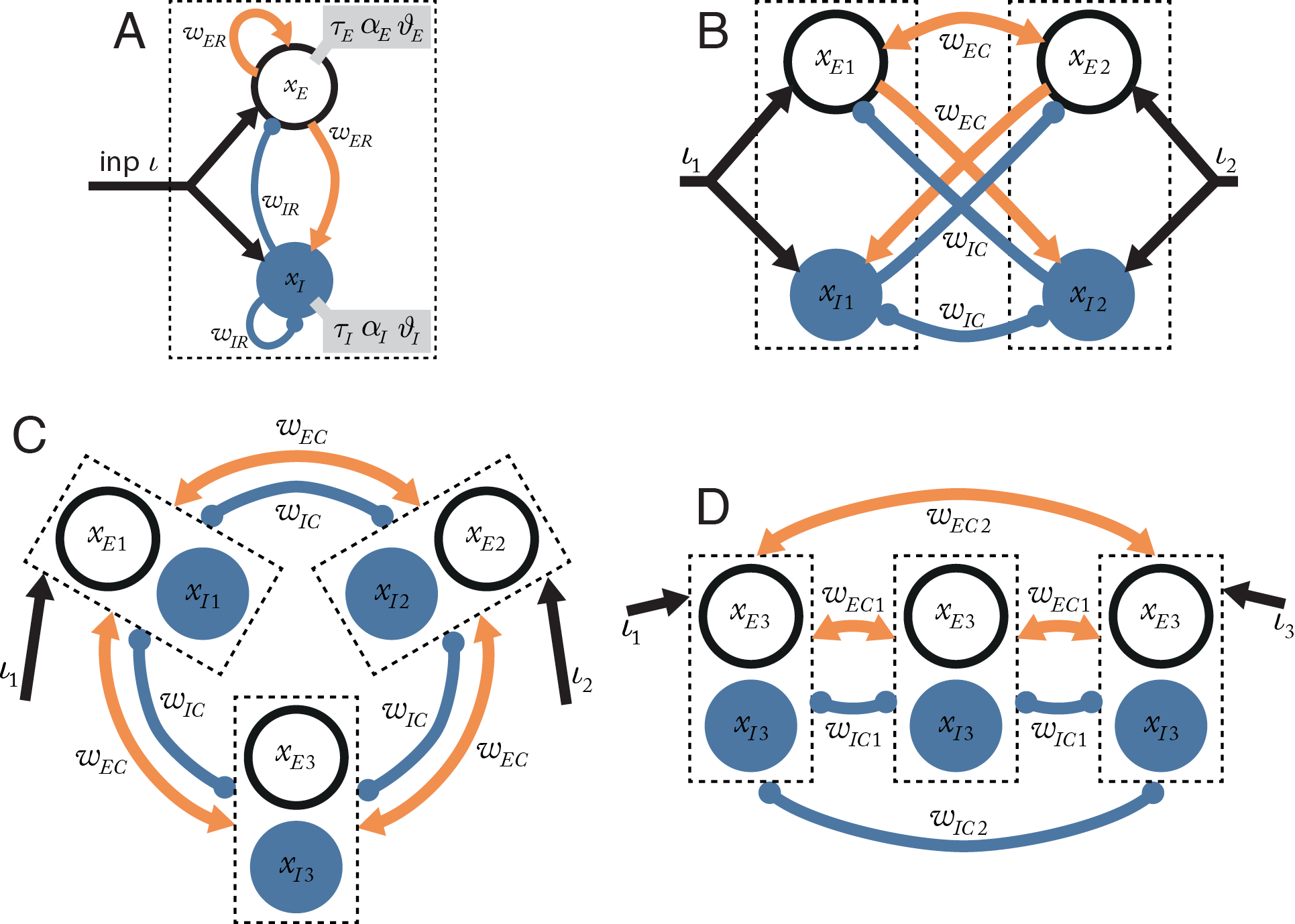
Figure 3: Analytical models for competition in cortex
Figure 4: Competition in linear networks
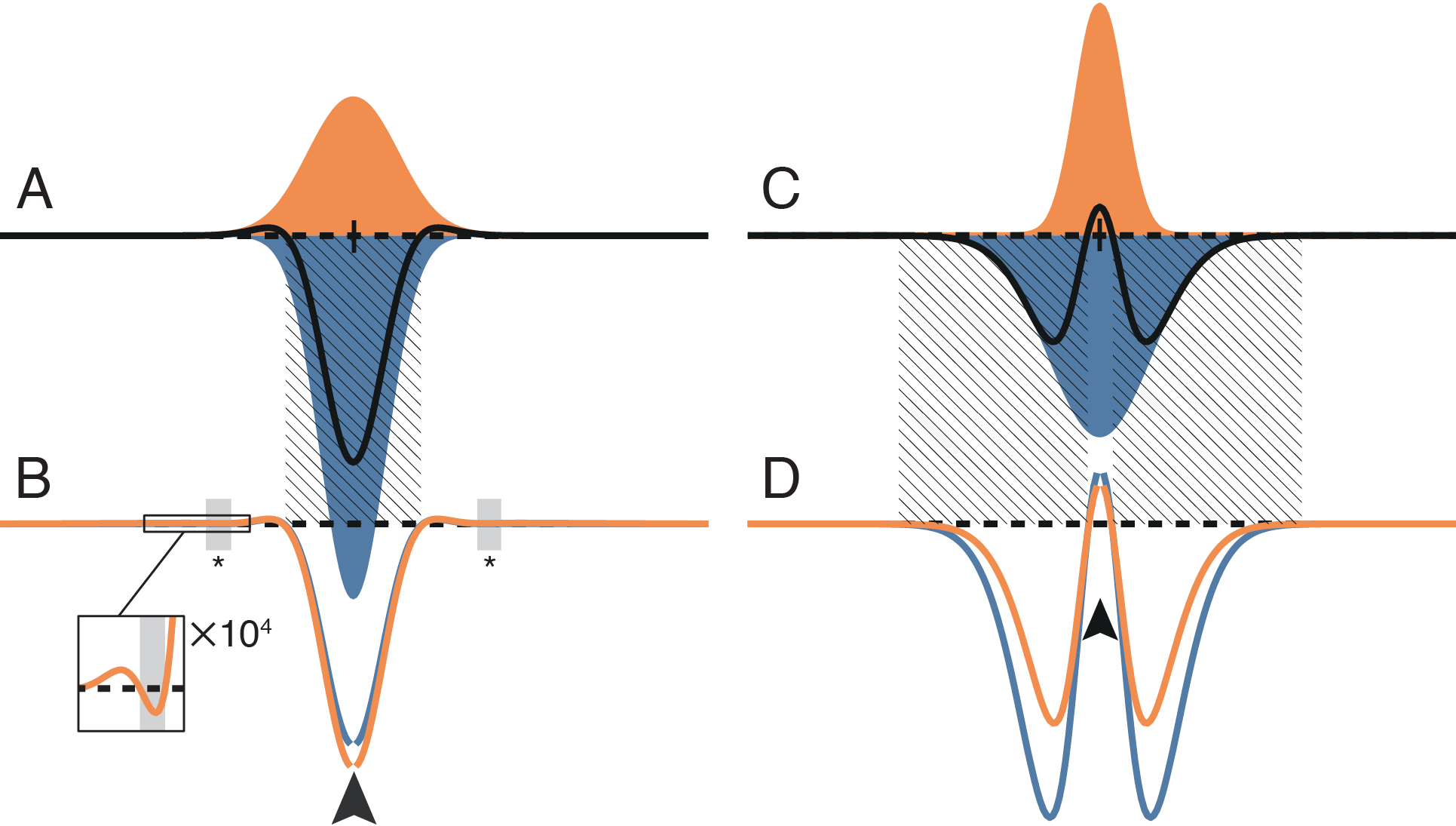
Figure 4: Competition in linear networks
Figure 5: Analytical predictions vs numerical simulations
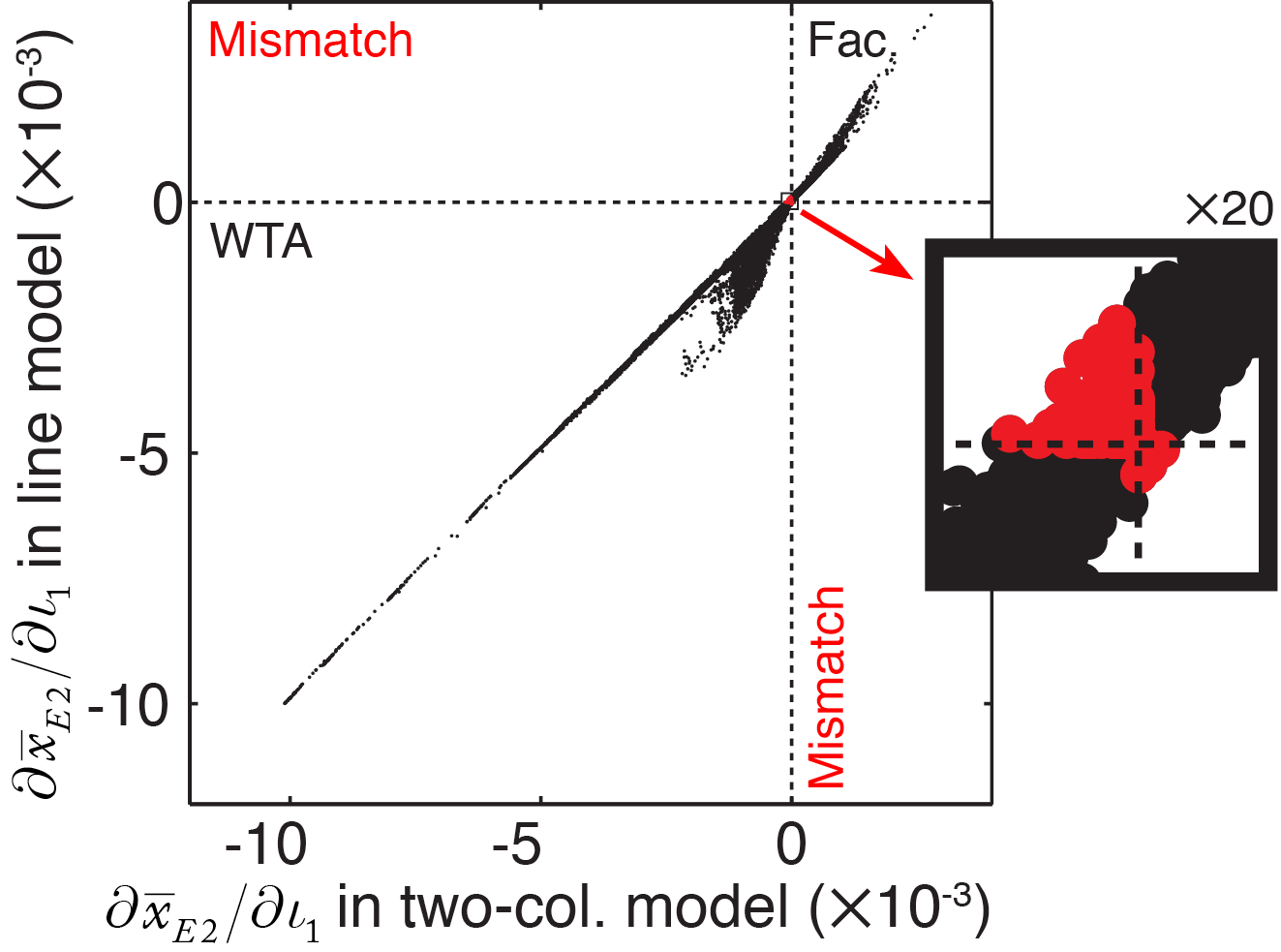
Figure 5: Analytical predictions vs numerical simulations
Competition is a well-studied and powerful mechanism for information processing in neuronal networks. However, many models for columnar cortex (cats and monkeys, for example) rely on long-range inhibitory interactions, which seem not to be present in the cortex. We explored whether competition can occur over long distances, with realistic cortical anatomy.
Models based on competitive interactions have been used to describe the shaping of functional properties in visual cortex, as well as the development of functional maps in columnar cortex. These models require competition within a cortical area to occur on a wider spatial scale than cooperation, usually implemented by lateral inhibitory connections having a longer range than local excitatory connections (a “mexican hat”; Figure 2A). However, measurements of cortical anatomy reveal that the spatial extent of inhibition is in fact more restricted than that of excitation (Figure 2B–C). Relatively few models reflect this, and it is unknown whether lateral competition can occur in cortical-like networks that have a realistic spatial relationship between excitation and inhibition.
Competition between columns
To seriously consider competition as a canonical computational mechanism for cortex, this potential conflict between model assumptions and cortical anatomy must be resolved. When is it possible for two points in columnar cortex to be in competition? We studied this question in very small networks that can be analyzed mathematically, and also via simulations of larger networks.
Analytical models
The concept of a cortical column is primarily functional (Mountcastle et al., 1955). In cat, monkey, ferret, tree shrew and many other higher mammals, neurons existing on a line perpendicular to the pia share many commonalities in their function. In this paper we take a column to be a small region within a neocortical area of a higher mammal, of the minimum size such that the function of each column is homogeneous but such that neighbouring columns can have different functions. This allows us to simplify the neurons in a column to a small population of interacting excitatory and inhibitory units. However, our simulations incorporate the fact that single columns make lateral projections to a large number of neighbouring columns, and receive input from a similar large number of neighbours. The function of our column model is discrete, but the virtual anatomical inputs and outputs of our columns are highly overlapping.
The foundation of the analytical models presented here is a simplified version of a cortical column, consisting of a coupled pair of an excitatory and an inhibitory linear-threshold unit (Wilson and Cowan, 1973; Landsman et al., 2012; Figure 3A). These units are designed to correspond in behavior to the average excitatory neuron and average inhibitory neuron in the small population of neurons within a single cortical column of very narrow width. The excitatory and inhibitory pair of units are assumed to exist at the same point on a cortical sheet, so that each unit has the same average self-connectivity as with the other unit of the pair.
The column dynamics are governed by the system of equations $$\tau_{E} \cdot \dot{x}_{E} + x_{E} = w_{ER} \cdot {\alpha}_{E} \left[ x_{E} - {\vartheta}_{E} \right]^{+} - w_{IR} \cdot {\alpha}_{E} \left[ x_{I} - {\vartheta}_{I} \right]^{+} + \iota$$ $$\tau_{I} \cdot \dot{x}_{I} + x_{I} = w_{ER} \cdot {\alpha}_{E} \left[ x_{E} - \vartheta_{E} \right]^{+} - w_{IR} \cdot {\alpha}_{E} \left[ x_{I} - {\vartheta}_{I} \right]^{+} + \iota$$ where \( x_{E} \) and \( x_{I} \) are the internal state of the excitatory and inhibitory unit in the pair; \( \left[x\right]^{+} \) denotes the linear-threshold transfer function \( \left[x\right]^{+}=\max\left(x,0\right) \); \( w_{ER} \) is the recurrent synaptic weight from an excitatory units to the units in the same column; \( w_{IR} \) is the recurrent synaptic weight from an inhibitory unit to the units in the same column; \( \tau_{n} \)is the time constant of unit \(n\); \( \alpha_{n} \) is the activation gain of unit n; \(\vartheta_{n} \) is the activation threshold of unit n; and \( \iota_{n} \)is the external input current to column \(n\).
Analysis method
We construct a set of differential equations embodying one of the columnar network models shown in Figure 3. Since the systems are piecewise-linear, a Jacobian of the system can be constructed for each linear partition in the state space defined by the activity of all units (Hahnloser, 1998). The real parts of the eigenvalues and trace of the Jacobians determine when the system is stable in a bounded input-bounded output (BIBO) sense. For the simple systems shown in Figure 3, the set of eigenvalues can be described analytically.
To determine whether two columns in a model are in competition, we measure the activity increase or decrease of activity in the excitatory unit in column 2 produced by an increase in the input to column 1 (i.e. \( \partial \bar{x}_{E2}/ \partial \iota_{1} \)). The value of this partial derivative depends on the system parameters, including the weights between the two columns. When the partial derivative is negative, then increasing the input to column 1 leads to a decrease in the activity of column 2, via disynaptic inhibition or other network effects. Due to the symmetric nature of our models, the same interaction would also occur in the reverse direction from column 2 to column 1. If increasing the input to either column decreases the activity of the other, then we say the columns are in competition. For our simple models we can find closed analytical forms for the partial derivative \( \partial \bar{x}_{E2}/ \partial \iota_{1} \) and so can solve for simple conditions on each of the system parameters that correspond to competitive interactions.
Analytical results
The question explored by the simple two-column model is simply: when can two points in columnar cortex be in direct competition, disregarding network connectivity external to the columns in question? By applying the analysis technique described above, we found that two points in a columnar system can only be in competition when the inhibitory coupling \( w_{IC} \) between the two columns is stronger than the excitatory coupling \( w_{EC} \). This is a strong result that does not depend on the thresholds for excitation and inhibition, nor on the time constants of excitation and inhibition
The two-column model neglects the effect of network interactions that might be mediated by additional columns. For example, competition between two distant points in a columnar system could be mediated by a third column placed at an intermediate location. We explored this possibility by designing networks containing three columns (Figure 3C–D).
We found, just as for the two-column model, that competition can only occur when the direct inhibitory coupling between the two columns is stronger than the direct excitatory coupling. A third column cannot provide a sufficient indirect inhibitory contribution to mediate competition. We call this the direct coupling effect: the interaction between two columns is primarily determined by direct excitatory and inhibitory coupling.
Simulation models
The simple analytical models were comprised of only few units, and directly modeled at most three columns. But how predictive are these simple models for a larger-scale 1D or 2D simulation composed of many columns, and with realistic spatial profiles of connectivity? We simulated linear and two-dimensional plate models composed of columns with the same structure as the basic analytical column. In place of simple point-to-point connectivity we introduced spatial profiles of synaptic connections based on Gaussian fields (Figure 4A and C), with synaptic parameters estimated from the experimental literature.
Competition in linear models
We examined the presence and absence of competition in these linear models by injecting a point excitatory stimulus into a single column of a quiescent network. Two locations are in competition if providing a positive input current to a source column results in a net suppressive effect on a target column, indicated by a net negative current arriving at the target column. Since the coupling patterns of our networks are homogeneous and symmetric, the effect of injecting a point excitatory stimulus is identical between any two locations on the network.
We found that under realistic spatial profiles of lateral excitation and short-range inhibition (Figure 4A–B), and under a mexican-hat arrangement with lateral inhibition (Figure 4C–D), the direct coupling effect predicted a central region of competition that matched the simulation results to within the spatial resolution of the simulation. However, in the case of lateral excitation a region of competition mediated by multi-columnar interactions emerged (asterisks and inset in Figure 4B). This competition occurred because a column activated by lateral excitation distant from the point stimulus can suppress activity locally through short-range inhibitory connections. However, since the gain of single synaptic connections is low, an effect relying on three or more synapses must also be comparatively weak. Under the realistic parameters simulated here, the scale of the multi-synaptic effect was at least four orders of magnitude weaker than that produced by the direct coupling effect.
Direct comparison with analytical results
To determine how well the two-column analytical predictions hold for an arbitrary homogeneous model, we directly compared the numerical predictions between a linear model and our two-column model configured with identical coupling strengths. We simulated 2500 linear models with Gaussian profiles of excitatory and inhibitory coupling (such as those shown in Figure 4), built with randomly-generated combinations of spatial ranges. We injected current into 50 pairs of columns in each model, and numerically computed the partial derivative \( \partial\bar{x}_{E2}/\partial\iota_{1} \) to measure the presence and strength of competition between the pair of columns. We then reduced the linear model to a two-column configuration, by removing all weights except those within and between the units in the pair of driven columns, and again computed the partial derivative.
Figure 5 shows the comparison between the strength of competition predicted under the two-column model and the strength of competition measured in the line model. The derivatives computed for the two-column model showed an impressive predictive power for the line model. A very small proportion of simulated line models exhibited competition when the two-column model predicted facilitation, and vice versa (highlighted points in Figure 5). However, all mismatches between two-column and line model results occurred close to the origin, where interactions between the two tested columns were very weak.
Conclusions
We found that the presence and strength of competition or cooperation between two columns was primarily determined by the direct excitatory and inhibitory coupling between those columns. We observed very slight deviations from our analytical expectations in 2D plate and 1D line models. However, the deviations due to multi-columnar network interactions were considerably weaker than the direct coupling effects predicted by our analytical models. We therefore expect that in a biologically realistic network or in cortex itself, the first-order direct coupling effects are likely to remain, while the small deviations from these effects are unlikely to be a significant factor in the face of the many noisy phenomena that influence a biological network.
Our results indicate that while lateral competition is difficult to justify in columnar cortical architectures, competition could nevertheless occur between neighbouring cortical columns over short distances (see Figure 4B). Recent work exploring competition and information processing in non-columnar (mouse visual) cortex (Muir et al., in revision), competition and learning within local populations (Jug et al., 2012) and dynamics of cortical columns with local inhibition (Landsman et al., 2012) show that local excitatory connectivity can provide a rich repertoire of complex dynamics and competitive behaviour for information processing in cortex.
Publications
This work was published in Neural Computation: DR Muir and M Cook. 2014. Anatomical Constraints on Lateral Competition in Columnar Cortical Architectures, Neural Computation 26 8:1624–1666. DOI: 10.1162/NECO_a_00613. Reprint: PDF.
Acknowledgements
The authors gratefully acknowledge Tom Binzegger, Kevan Martin and Rodney Douglas for providing the data in Figure 2 (Binzegger et al., 2007). The authors would like to thank Rodney Douglas for spurring this work on in its early stages. The authors would also like to thank the participants of the Winner-Take-All and Neural Computation work groups at the Capo Caccia meeting, who have provided a stimulating environment for discussion of this work and on cortical computation in general.
Funding
This work was funded by a John Crampton Travelling Fellowship to DRM, by the European Commission (FP6-2005-015803 DAISY) by the Velux Stiftung and by CSN fellowships to DRM.