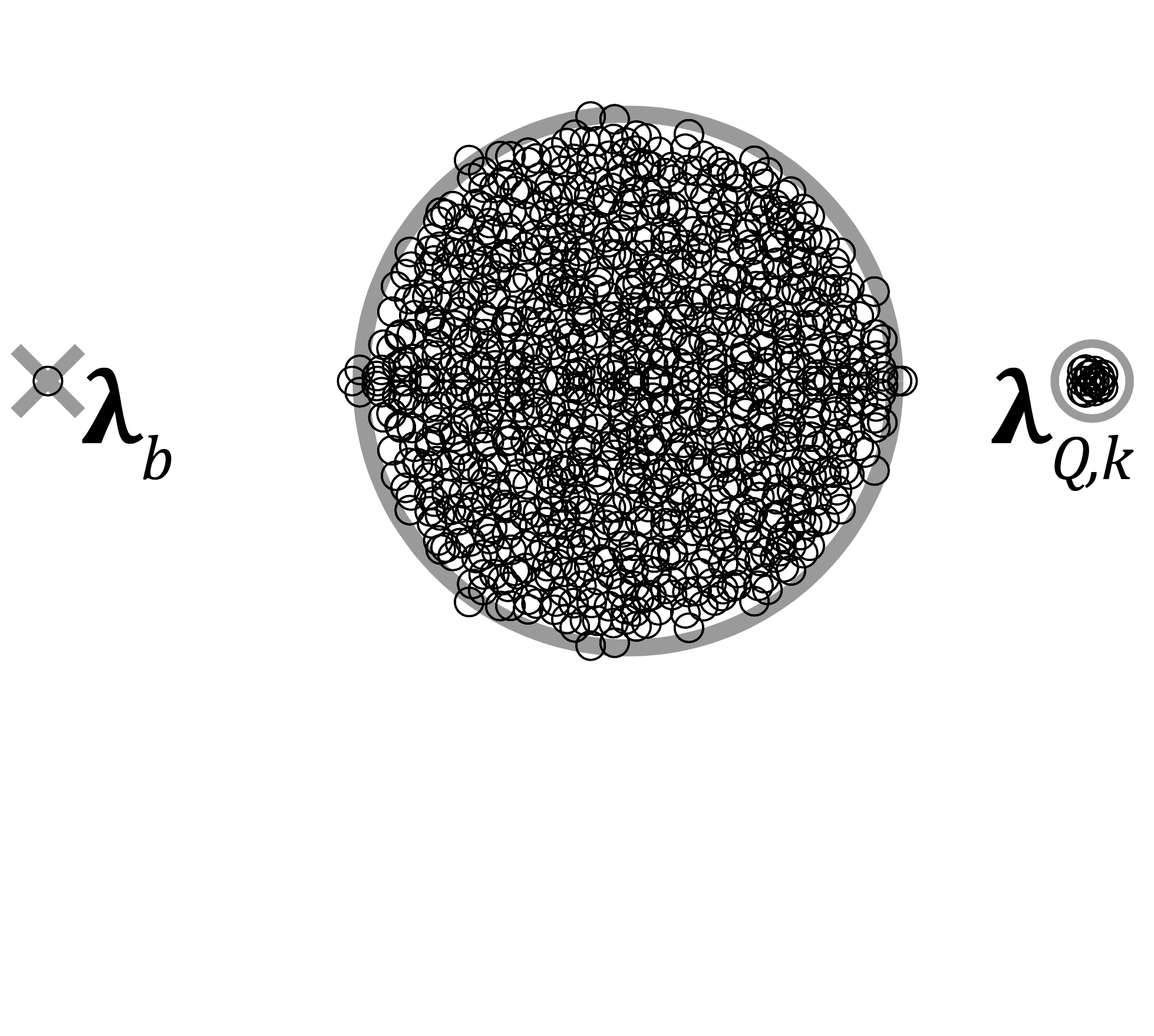
How does the behaviour and stability of a neuronal network depend on the connectivity rules used to build it? A common approach is to build many stochastic instances of a network, tweak the parameters, simulate and analyse, and then try to derive an impression about stability. We instead used an analytical approach, to directly relate connectivity rules and parameters to bounds on stability.

Examining the eigenvalues of the network weight matrix — a set of numbers that are descriptive of the matrix structure — can also provide information about how stable a given stochastic network is. However, this requires a computationally expensive numerical analysis to be performed, which is unfeasible for very large networks.

In any case, either approach — analysing simulations or analysing eigenvalues — only provides information about the particular network under examination, and gives no guarantee about future randomly-generated networks. We instead used the mathematical rules used to define a family of stochastic network models to derive analytical bounds on the expected eigenvalues for that family. As a consequence, we can say in advance for a given set of parameters whether networks built using those parameters will be stable. We can also make some basic statements about computational behaviour: in particular, whether competition exists and how strong that competition is.

Cortical bias

Much of my recent work has examined how rules for biased (or “specific”) excitatory connections influence cortical behaviour. Here we proposed two network architectures, embodying alternative rules for biased excitatory connections.

Stochastic community structure

Many man-made and biological networks contain clustering of connections, such that “communities” of nodes which are more tightly coupled emerge (Girvan & Newman 2002). In mammalian neocortex, for example, connections between neurons in cortex are not made randomly, even ignoring any dependence on physical location. Excitatory neurons in rodent cortex form subnetworks within which connections are made more densely (Yoshimura & Callaway 2005; Ko et al. 2011; Li et al. 2012).

We therefore define a number of subnetwork blocks, \( M \), that equally partition the excitatory population. Each excitatory node \( i \) is assigned to a subnetwork with ID \( v_{i}:\left(1..M\right) \), with each subnetwork containing \( \left(1-f_{I}\right)N/M \) excitatory nodes. We define the elements of the subnetwork block membership matrix as \( q_{m;ji}\in Q_{m} \), where $$q_{m;ji}=\left\{ \!\!\begin{array}{cl}\mathrm{1} & \textrm{if }v_{i}=v_{j}=m\textrm{ and }i,\, j\textrm{ are excitatory,}\\ \mathrm{0} & \textrm{otherwise.}\end{array}\right.$$

The matrix \( Q_{m} \) is therefore a \( N\times N \) boolean matrix indicating possible excitatory to excitatory connections within a single subnetwork \( m \). Connections within and between subnetworks are governed by a global parameter \( r \), which defines the proportion of total connections weight for each excitatory node that is restricted to be made within each subnetwork (with \( 0\leq r\leq1 \)).

Spatial and functional connectivity constraints

Pair-wise interactions in physical networks can depend on distance, such that the strength or probability of interaction is related to physical distance via a function over Euclidean space. Random matrices that incorporate this constraint are known as Euclidean Random matrices (Mezard et al. 1999). Neurons in the neocortex reside in physical space, with connection probabilities modulated smoothly across the cortical surface (Holmgren et al. 2003; Binzegger et al. 2007; Boucsein et al. 2011). In addition, connections within the cortex are modulated by functional similarity over one or more physiological metrics — in many mammalian species, neurons (or small regions of cortex) that have similar functional metrics are more likely to be connected (see the superficial patch system; Muir et al. 2011; Ko et al. 2011; Cossell et al. 2015).

In our networks, each neuron \(i\) is randomly assigned a location vector \(\mathbf{x}_{i}\) sampled uniformly from the unit hypercube with dimensionality \(D\), such that \(\mathbf{x}_{i}=\left\{ x_{i,1},x_{i,2},\ldots,x_{i,D}\right\} \) and \(x_{i,k}\!\sim\!\mathrm{Uniform}\!\left(0,1\right)\). The matrix \(s\!_{ji}\in S\), which contains connection weights defined by spatial and functional relationships, is a Euclidean random matrix with \(s\!_{ji}=\mathcal{F}\!\left(\mathbf{x}_{i},\mathbf{x}_{j}\right)\), where \(\mathcal{F}\!\left(\cdot\right)\) is a function defining the connection weight according to a similarity metric relating the location of nodes \(i\) and \(j\) (Mezard et al. 1999).

In this work we consider a smooth connectivity relationship in a multi-dimensional space: a \(D\)-dimensional Gaussian, such that $$\mathcal{F}\!\left(\mathbf{x}_{i},\mathbf{x}_{j}\right)=\mathcal{G}\!\left(\left\Vert \mathbf{x}_{i}-\mathbf{x}_{j}\right\Vert ^{\circ}\right)=\exp\!\left(\!\!-\frac{\left\Vert \mathbf{x}_{i}-\mathbf{x}_{j}\right\Vert ^{\circ2}}{D^{2}\kappa^{2}}\right)\textrm{,}$$ where \(\left\Vert \mathbf{x}_{i}-\mathbf{x}_{j}\right\Vert ^{\circ2}\) is the squared 2-norm distance over a unit hyper-torus. Connectivity in this network is under the control of a parameter\(\kappa\), which determines the range of connectivity within the network \(\left(\kappa>0\right)\). As \(\kappa\) increases, so does the spatial and functional range over which connections are distributed.

Eigenvalue spectra of sparse matrices with stochastic community structure

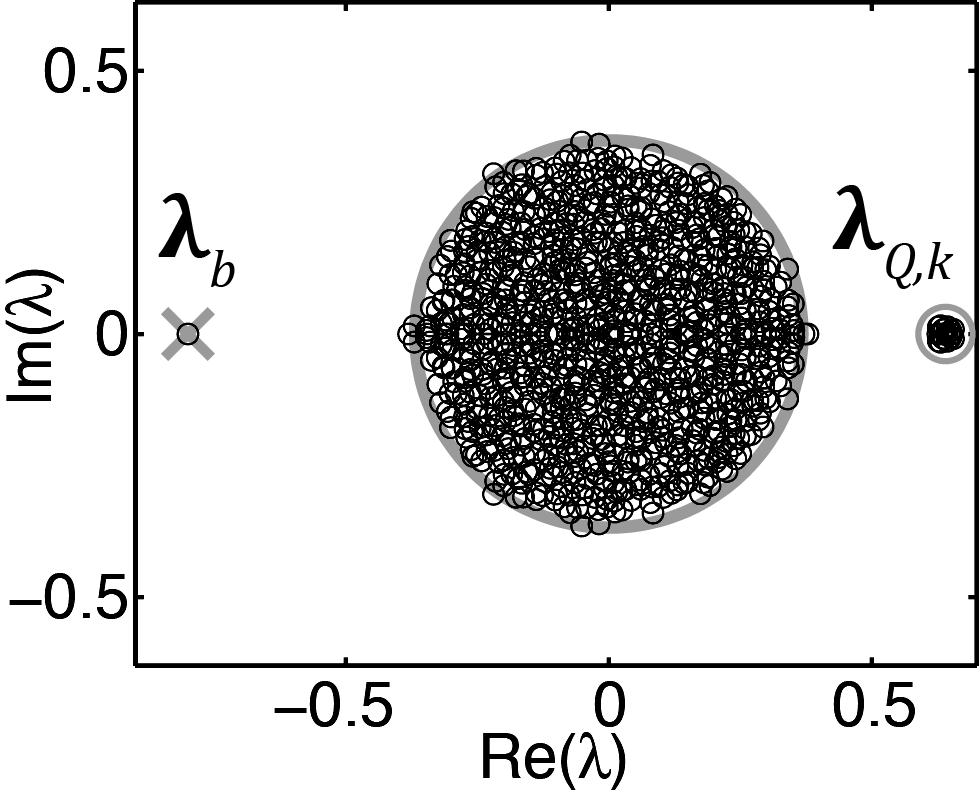
The weight matrix \(W\) has a trivial eigenvalue \(\lambda_{b}=w_{E}\left(1-f_{I}\right)-w_{I}f_{I}\), determined by the global balance between excitation and inhibition in the network (Fig. 1; Rajan & Abbott 2006; Muir & Cook 2014). Including modular stochastic structure introduces a number of non-zero, positive eigenvalues related to the number of subnetworks \(M\) and the strength\(r\) of within-subnetwork connectivity: \(M-1\) eigenvalues are located at \(\lambda_{Q}=\Sigma W_{SSN}-\Sigma W_{NS}=w_{E}\left(1-f_{I}\right)r\). The subnetwork-related eigenvalues \(\lambda_{Q,k}\) are distributed within a circle of radius \(\sigma_{\mathbf{Q}}\) centered at \(\lambda_{Q}\), where \(\sigma_{\mathbf{Q}}\) is the standard deviation of the subnetwork connection weights (Fig. 1).

As connectivity in the network becomes more sparse then the non-trivial and non-subnetwork eigenvalues become densely clustered within a circle centered at the origin, bounded in expectation by an outer radius related to the variances of the elements of \(W\) (Fig. 1; Rajan & Abbott 2006).

Eigenvalues of matrices describing networks with spatial connectivity constraints

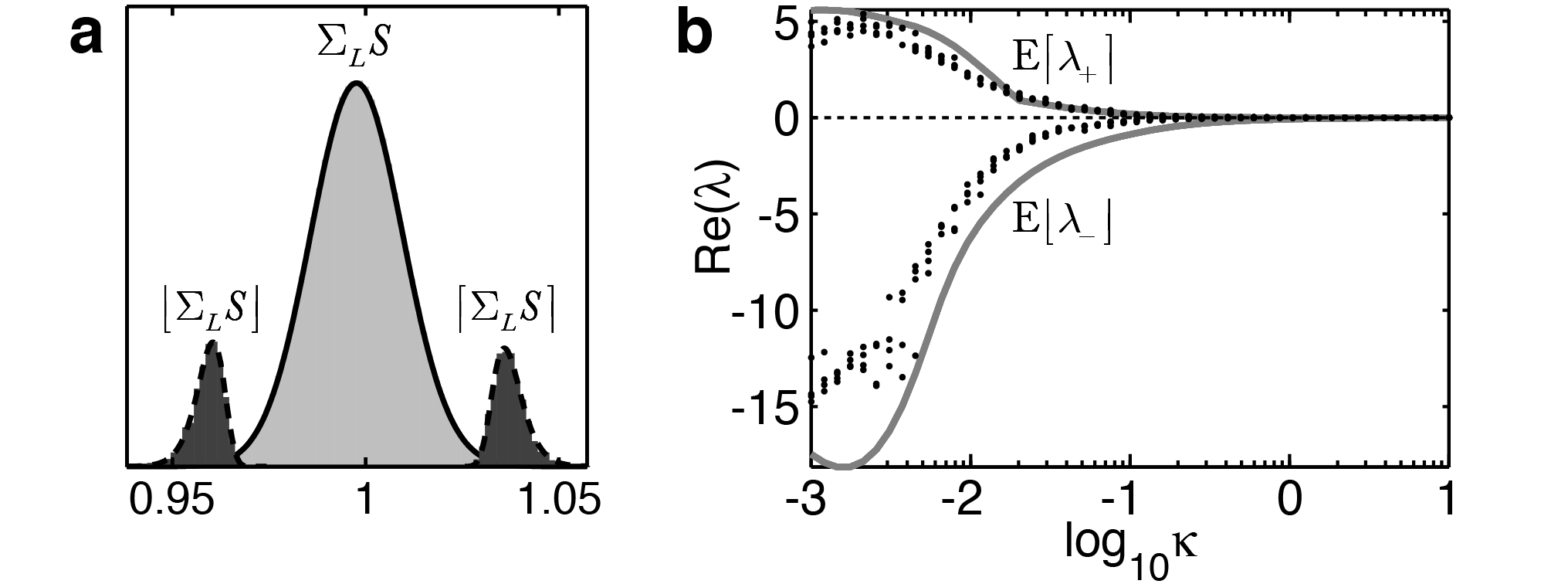
We then examined the eigenvalues of matrices describing networks that included a connection constraint over spatial proximity or functional similarity. This connection profile serves to strongly couple each node to a group of nearby nodes, with the size of the group decreasing as \(\kappa\rightarrow0\). We therefore approximate a portion of \(W\) for a small strongly-coupled partition by a pair of excitatory and inhibitory neurons (Landsman et al. 2012), with $$\left.W\right|^{P}\!=\left[\begin{array}{cc} \left.W_{EE}\right|^{P} & \left.-W_{EI}\right|^{P}\\ \left.W_{IE}\right|^{P} & \left.-W_{II}\right|^{P} \end{array}\right]\approx\left[\begin{array}{cc} \hat{w}_{ee} & -\hat{w}_{ei}\\ \hat{w}_{ie} & -\hat{w}_{ii} \end{array}\right]\textrm{,}$$ where \(\hat{w}_{*}\) denotes estimates for the means of the corresponding sub-matrices in \(\left.W\right|^{P}\). The eigenvalues of \(\left.W\right|^{P}\) have the form \(2\lambda_{\pm}=\hat{w}_{ee}-\hat{w}_{ii}\pm\left[\left(\hat{w}_{ee}+\hat{w}_{ii}\right)^{2}-4\hat{w}_{ei}\hat{w}_{ie}\right]^{{1}/{2}}\).

We obtain closed form estimates for the distribution of \(\left\{ \lambda_{+},\,\lambda_{-}\right\}\) by examining the most extreme values of \(\hat{w}_{*}\). We denote the maximum estimate of a parameter by \(\left\lceil \cdot\right\rceil\), and the minimum estimate as \(\left\lfloor \cdot\right\rfloor\). We estimate the eigenspectrum bounds as $$2\left\lceil \lambda_{+}\right\rceil=\left\lceil \hat{w}_{ee}\right\rceil-\left\lfloor \hat{w}_{ii}\right\rfloor+\left[\left(\left\lceil \hat{w}_{ee}\right\rceil+\left\lfloor \hat{w}_{ii}\right\rfloor \right)^{2}-4\left\lceil \hat{w}_{ie}\right\rceil\left\lfloor \hat{w}_{ei}\right\rfloor \right]^{{1}/{2}}\textrm{and}\\ 2\left\lfloor \lambda_{-}\right\rfloor=\left\lfloor \hat{w}_{ee}\right\rfloor-\left\lceil \hat{w}_{ii}\right\rceil-\left[\left(\left\lfloor \hat{w}_{ee}\right\rfloor+\left\lceil \hat{w}_{ii}\right\rceil \right)^{2}-4\left\lfloor \hat{w}_{ie}\right\rfloor\left\lceil \hat{w}_{ei}\right\rceil \right]^{{1}/{2}}\textrm{.}$$

To obtain estimates for \(\hat{w}_{*}\), we derive the distribution of sums of \(L\) elements of \(S\) (denoted \(\Sigma_{L}S\)). The extremal values of sums \(\Sigma_{L}S\) for \(i\neq j\) (see Fig. 2a) are distributed according to $$\left\lceil\Sigma_{L}S_{i\neq j}\right\rceil\hat{\sim}\frac{\Gamma_{G}\left(\alpha_{D},0,{x}/{\theta_{D}}\right)^{L-1}\hspace{-1em}}{\Gamma\left(\alpha_{D}\right)} \exp\left({-x}/{\theta_{D}}\right)Lx^{-1+\alpha_{D}}\theta_{D}^{-\alpha_{D}} \textrm{ and}\\ \left\lfloor \Sigma_{L}S_{i\neq j}\right\rfloor\hat{\sim\,}\frac{\Gamma_{R}\left(\alpha_{D},{x}/{\theta_{D}}\right)^{L-1}\hspace{-1em}}{\Gamma\left(\alpha_{D}\right)} \exp\left({-x}/{\theta_{D}}\right)Lx^{-1+\alpha_{D}}\theta_{D}^{-\alpha_{D}}\textrm{,}$$

The partition estimates for \(\hat{w}_*\) (see Fig. 2b) are described by \(\hat{w}_{ee}\hat{\sim}w_{E}\left(s_{ii}+\Sigma_{\left(1-f_{I}\right)N-1}S\right)\), \(\hat{w}_{ii}\hat{\sim}w_{I}\left(s_{ii}+\Sigma_{f_{I}N-1}S\right)\), \(\hat{w}_{iw}\hat{\sim} w_{E}\left(\Sigma_{f_{I}N}S\right)\) and \(\hat{w}_{ei}\hat{\sim} w_{I}\left(\Sigma_{\left(1-f_{I}\right)N}S\right)\), where the notation \(\vartheta\hat{\sim} P\left(x\right)\) indicates that \(\vartheta\) is distributed proportional to function \(P\left(x\right)\).

Discussion

In networks with modular stochastic structure, the subnetwork eigenvalues \(\lambda_{Q,k}\) correspond to eigenvectors that express competition between subnetwork partitions. The presence of these eigenvectors implies that if a partition is active, it will tend to decrease the activity of the other subnetworks. If these eigenvalues correspond to unstable modes (i.e. \(\lambda_{Q}>1\)) then the competition eigenvectors are unstable and the corresponding nonlinear network will be characterized by hard competitive interactions between subnetworks (Coultrip et al. 1992; Muir & Cook 2014). Our results indicate that in the absence of an inhibitory contribution to subnetwork membership, the subnetwork eigenvalues \(\lambda_{Q}\) are not dependent on global inhibitory feedback. Increasing the strength of inhibition cannot therefore balance the effect of introducing modular connectivity to a network. This surprising result suggests that hard limits exist on the degree of subnetwork specificity allowable for synaptic connections in cortex.

Our results for networks with smooth spatial and functional connectivity indicate that as the spatial range of interactions decreases, they become increasingly sensitive to the local balance between excitation and inhibition, in the form of excitatory recurrence (\(\hat{w}_{ee}\)) and excitatory / inhibitory recurrent connections \(\hat{w}_{ie}\) and \(\hat{w}_{ei}\).

Our results highlight the importance of excitatory and inhibitory balance, not only globally but also at the meso-scale of local network statistics. Since our connectivity constraints can be treated as functional similarity constraints over some physiological measure, we expect that homeostatic plasticity mechanisms in cortex must be sensitive to balance within functional cohorts.

Publications

This work was published in Physical Review E: DR Muir and T Mrsic-Flogel. 2015. Eigenspectrum bounds for semi-random matrices with modular and spatial structure for neural networks, Phys. Rev. E 91, 042808. DOI: 10.1103/PhysRevE.91.042808.

Acknowledgements

We thank L Cossell, A Landsman, M Pfeiffer, M Penny, M Okun and P Latham for helpful discussions. This work was supported by the University of Basel Young Researchers fund.