Fast Loop mesh subdivision in matlab
30th September, 2011Progressive subdivision of a surface
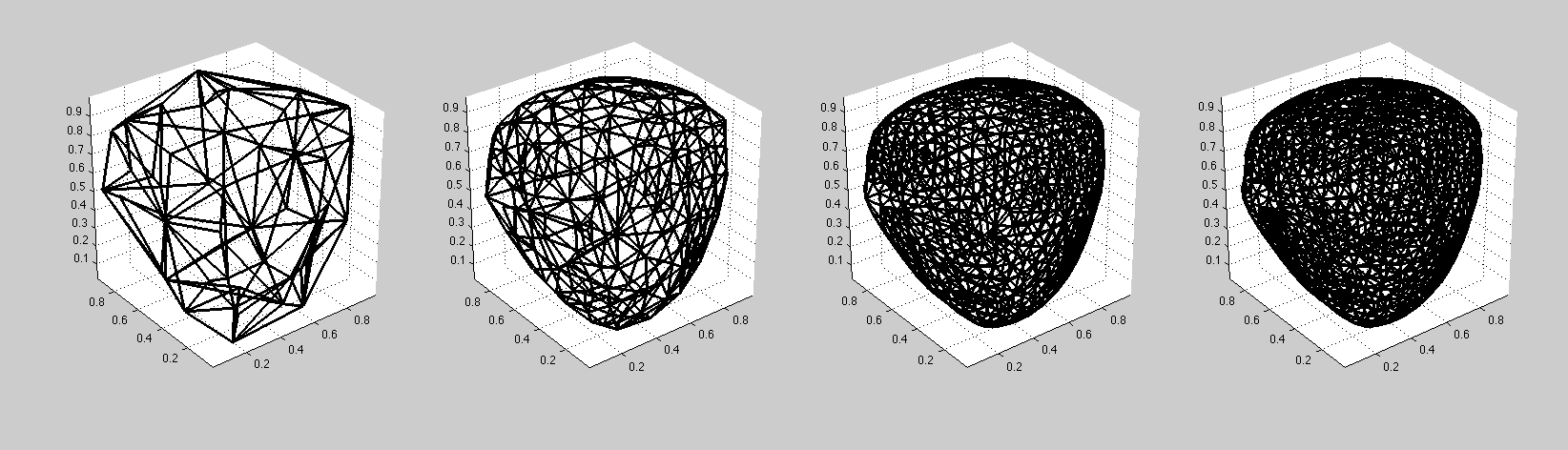
Progressive subdivision of a surface
This matlab function sub-divides surface meshes, using the Loop subdivision algorithm. Because this algorithm is based on B-spline curve continuity, the surface is smoothed with only small distortions. The boundary of the surface is also left essentially undistorted.
Download and install
Download the Loop subdivision function, and save it into a directory on your Matlab path.
Usage
[mfRefinedMesh, mnTriangulation] = ...
LoopSubdivisionLimited( mfMeshPoints, mnTriangulation, fMinResolution, vbBoundaryEdges)
mfMeshPoints is an Nx3 matrix, each row of which [x y z] defines a point in three-dimensional space. mnTriangulation is an Mx3 matrix, each row of which [m n p] defines a triangle existing on the surface, where m, n and p are indices into mfMeshPoints.
fMinResolution defines the desired minimum length of an edge in the final subdivision. Edges shorter than fMinResolution will not be divided further.
The optional argument vbBoundaryEdges identifies which edges should be treated as boundary edges (and so should their locations should be attempted to be maintained by the algorithm). This argument will be calculated by the algortihm if it is not supplied.
mfRefinedMesh will be a Px3 matrix, each row of which specifies a vertex in the subdivided mesh. mnTringulation will be a Rx3 matrix, each row of which specifies a surface triangle in the subdivided mesh.
Algorithm from [1].
Room for improvement
If you work out how to maintain the vertex and edge adjacency matrices through a full subdivision run, then great! That would speed up subsequent runs a great deal, since a lot of the time is spent computing the edge adjacency matrix...
References
[1] Loop, C 1987. "Smooth subdivision surfaces based on triangles." M.S. Mathematics thesis, University of Utah. [pdf]